3. 통계의 기초분석

3.1 빈도분석

빈도분석은 설문조사의 결과에 대한 가장 중요한 기초 정보를 제공해 줍니다.

예를 들면 성별의 경우 남자가 몇 %인지 여자가 몇 %인지 알려주는 기능을 하며

남자와 여자의 평균값이나, 최대값, 최소값, 사분위수, 중위값 등 다양한 통계량을 제시해 줍니다.

보고서를 작성하는 경우라면 반드시 빈도와 비율을 동시에 제시해 주는 것이 좋습니다.

빈도분석은 모든 척도에 사용이 가능하지만 등간척도와 비율척도로 구성된 변수는 적절한 구간으로 리코딩한 후 사용하는 것이 좋습니다.

빈도분석에는 생각보다 다양한 분석을 할 수 있고 다양한 그래프와 도표를 만들 수 있으므로 가장 기초적이면서도 꼭 필요한 분석입니다.

여기서 빈도분석에 대해 자세히 알아보기 위해 [예제 04-1]를 가지고 연습해 봅시다.

1) 시작방법

SPSS 주메뉴 중 [분석]메뉴에는 다양한 통계분석기법이 있습니다. 그 중에서 [기술통계량]의 [빈도분석]을 찾아 클릭을 하면 됩니다.

우선, [예제 04-1]를 불러옵니다. 빈도분석을 시작하기 위해 다음 절차를 따릅니다.

분석(A)→기술통계량(E)→빈도분석(F)

절차를 따르면 [그림 3.1]와 같은 창이 나타납니다.

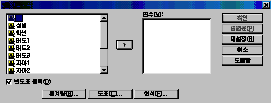
빈도분석에는 통계량(S), 도표(C), 형식(F)의 세 종류가 있습니다. 이에 대해 자세히 살펴보겠습니다.

종 류

내 용

통계량(S)

중심경향(평균, 중위수, 최빈값, 합계), 백분위수 값(사분위수, 절단점, 백분위수), 산포도(표준편차, 최소값, 최대값, 분산, 범위, 평균의 표준오차), 분포(외도, 첨도) 등의 통계량을 설정할 수 있습니다.

도표(C)

막대도표, 원도표, 히스토그램 등 도표의 형식을 설정할 수 있습니다.

형식(F)

어떤 순서대로 출력할 것인지의 출력순서와 다중변수, 표 출력 범주를 설정할 수 있습니다.

① 통계량(S)의 내용

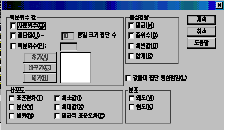
◎ 백분위수 값 : 한 집단의 분포에서 나타나는 누적된 백분율을 말합니다.

사분위수(Q)

사분위수는 100%를 4개의 범주로 나눈 값은 25%, 50%, 75%의 백분율에 해당하는 변수값이 얼마인지를 알려줍니다.

절단점(U)

사례들을 본인이 원하는 크기의 집단을 설정한 후 각 집단별 변수값이 얼마인지를 알려줍니다.

백분위수(P)

본인이 원하는 %를 설정하면 그에 대한 변수값을 알려줍니다.

◎ 집중경향 : 한 집단의 분포에서 나타나는 특성을 종합하고 요약하여 그 집단의 전체적인 경향을 알려주는 통계기법입니다.

보통 가장 많이 사용하는 것이 평균이고, 다른 것은 필요에 따라 사용하는 경향이 있습니다.

평균(M)

우리가 흔히 생각하는 평균값입니다.

중앙값(D)

전체 사례 중에 50%에 위치하는 값입니다.

최빈값(O)

전체 사례 중에 가장 많은 빈도를 차지하는 값입니다.

합계(S)

전체 사례를 모두 합한 값입니다.

◎ 산포도 : 한 집단의 분포가 평균 또는 중앙값에서 얼마나 떨어져 있는지(분산되어 있는지)를 알려주는 통계기법입니다.

표준편차(T)

분산에 제곱근(√)을 한 값으로 평균으로부터 떨어진 거리를 표준화한 값입니다.

분산(V)

평균에서 떨어진 값에 제곱을 한 후 모두 더한 값을 전체의 사례수로 나누어 준 값입니다.

최대값(I)

모든 사례 수에서 가장 큰 값입니다.

최소값(X)

모든 사례 수에서 가장 작은 값입니다.

범위(N)

전체 사례 수의 값들의 범위로 최대값과 최소값의 사이의 거리를 말합니다. 보통 [최대값-최소값+1]로 계산합니다

평균의 표준오차(E)

각 표본들의 평균들의 표준편차를 말합니다.

◎ 분포 : 정상분포의 곡선인지 아닌지 성향을 나타내 줍니다.

외도(W)

정상분포 곡선이 좌?우로 기울어진 정도를 말합니다. 정상분포의 경우 외도값이 0이며 좌측으로 기울어지면 (+)값으로 우측으로 기울어지면 (-)값으로 나타납니다.

첨도(K)

정상분포 곡선이 뾰족한 편인지 완만한 편인지를 알려줍니다. 정상분포의 경우 첨도값은 0이며 뾰족한 편일수록 (+)값으로 완만한 편일수록 (-)값으로 나타납니다.

② 도표(C)

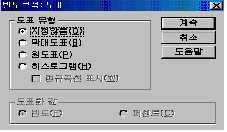
빈도분석에서 도표는 3가지 형식으로 이루어져 있습니다. [그림 3.3]에서와 같이 막대도표(B), 원도표(P), 히스토그램(H)로 이루어져 있고,

도표값을 빈도로 구성할지 비율(%)로 구성할지 설정할 수 있습니다.

③ 형식

빈도분석에서 형식은 결과를 일정한 순서에 따라 정렬할 수 있습니다. 변수가 여러 개인 경우 변수들을 비교할 것인지

각 변수별로 출력결과를 나타낼 것인지 설정할 수 있으며 표 출력범주 제한도 설정할 수 있습니다.

2) 실행방법

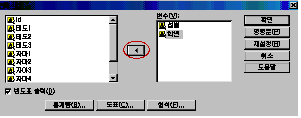
빈도분석의 옵션을 설정한 다음 빈도분석 대화상자 창에서 분석하기를 원하는 변수를 마우스로 클릭하여 선택한 후

가운데에 있는 화살표 버튼을 누르거나 더블 클릭하면 옆의 변수(V) 칸에 옮겨집니다. 그리고 나서 확인을 누르면 [그림 3.6], [그림 3.7]과 같은 결과 창이 나타납니다.

뷰어를 구성하는 두 개의 화면 중 왼쪽 화면은 통계분석결과 및 도표들의 제목으로 구성되어 있는데 이 제목을 클릭하면

그에 해당하는 분석결과 위치로 빠르게 이동할 수 있습니다.

3.2 기술통계분석

기술통계분석은 등간․비율척도에 대한 정보를 잘 요약․정리해주는 기능입니다. 예를 들어 나이에 관한 문항인 경우

대상자의 평균 나이가 40살이라고 제시한다면 그 결과물을 보는 사람이 이해하기 쉬울 것입니다.

게다가 기술통계분석을 하게 되면 정규분포성을 검증할 수 있으며, 각 변수들 값들을 표준화할 수 있습니다.

기술통계분석과 빈도분석의 차이점을 살펴보면, 빈도분석의 경우 주로 명목․서열변수 같은 이산적 데이터를 분석할 때 사용하고

, 기술통계분석은 주로 등간․비율변수와 같은 연속적 데이터를 분석할 때 사용합니다.

1) 시작방법

빈도분석과 비슷하게 [분석(A)]메뉴에서 [기술통계량]을 거쳐 [기술통계]를 찾아 클릭합니다.

우선, [예제 04-2]를 불러옵니다. 빈도분석을 시작하기 위해 다음 절차를 따릅니다.

분석(A)→기술통계량(E)→기술통계(D)

위의 절차를 따르면 [그림 3.8]과 같은 창이 나타납니다.

2) 실행실행

[그림 3.8]을 보면 옵션에 관한 것이 있습니다. 이 옵션을 통해 여러 가지 기능을 설정해 주면 됩니다.

이에 대해서 자세히 다뤄 봅시다. 여기서는 나이에 관한 변수를 [변수(V)]창으로 옮긴후 옵션을 설정합니다. 그럼 옵션에 대해 자세히 알아봅시다.

① 옵션

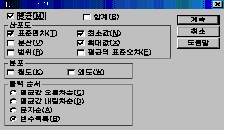
옵션에는 평균․합계, 산포도, 분포, 출력순서로 구성되어 있습니다. 빈도분석에서와 같은 기능을 하는 영역이므로 기초적인 분석이 가능합니다.

빈도분석과는 달리 도표나 그래프를 그릴 수 없습니다.

옵션에서 평균, 표준편차, 최소값, 최대값, 변수목록에 클릭을 해 본 후 계속을 누릅니다.

그러면 [그림 3.10]와 같은 출력결과창이 나타납니다.

3) 표준화된 값을 변수로 저장

표준화라는 것은 표준화된 평균편차를 말합니다. 만약에 A와 B 집단이 있다고 할 때 A집단의 나이평균이 30이고 B집단의 나이평균이 32라고 합시다.

여기서 B집단에 있는 사람들의 나이가 더 많다고 말할 수 있습니까? 그렇게 말할 수는 없죠. 이렇게 평균이나 표준편차 하나만을 가지고 두 집단을 비교할 수는 없습니다.

따라서 이런 경우 그 집단의 평균을 0, 분산을 1로 만들어 주어 평균편차를 표준화해 주어야 합니다.

그러기 위해 변수값을 표준화된 값으로 변환시켜주는 것이 중요합니다. 그러면 이전에 나이에 대한 변수를 표준화된 값으로 변환하여 저장하여 봅시다.

기술통계의 대화상자창(분석→기술통계량→기술통계)으로 가서 그 창에 있는 [□표준화된 값으로 저장]을 클릭한 후 계속을 누르면

[그림 3.11]과 같이 표준화된 점수값이 나타납니다. 평균이 0이므로 각각의 값이 평균보다 큰지 작은지를 뚜렷하게 구별할 수 있습니다.

3.4 평균비교

여기까지는 빈도분석과 기술통계분석을 통해 다양한 통계량을 구하는 방법에 대해 알아보았습니다.

이번에는 독립변수에 따른 종속변수의 평균이 얼마인지에 대해 알아봅시다. 남자와 여자의 나이에 대한 평균과 표준편차가 얼마인지

동시에 알아보기 위해 평균비교를 해야 합니다. 물론 다양한 통계방법(T검증, 변량분석 등)을 통해서도 구할 수 있지만,

그것은 뒤에서 다루도록 하고 간단히 평균비교를 해 봅시다. 우선, [예제 04-2]를 가지고 따라해 봅시다.

1) 시작방법

평균분석을 시작하기 위해서는 아래와 같은 절차를 따르면 됩니다.

분석(A)→기술통계량(E)→빈도분석(F)

위의 절차를 따르면 [그림 3.12]와 같은 대화상자가 나타납니다.

[그림 3.12] 대화상자를 보면 독립변수(D)와 종속변수(I)가 있습니다. 각각의 칸에 적절한 변수를 넣으면 됩니다.

그 외에도 레이어와 옵션(O)으로 구성되어 있습니다. 레이어는 세 변수 이상 분석할 때에 사용하는 것인데,

여기서 다루기보다는 교차분석에서 다루도록 하겠습니다. 옵션의 경우 중앙값, 표준편차 등의 통계량을 선택할 수 있도록 구성되어 있습니다.

2) 실행방법

독립․종속변수와 옵션 등을 모두 설정한 후에 확인을 누르면 [그림 3.13]과 같은 결과출력창에 케이스 처리 요약과 보고서가 나타납니다.

케이스 처리 요약에서는 통계분석에 사용한 사례수(포함)의 크기와 무응답(제외)의 크기와 비율(%)을 알려줍니다.

보고서에서는 변수와 각각의 사례수, 평균, 표준편차 값이 나타납니다. 남자의 경우 평균이 35.25, 표준편차가 7.14이고, 여자의

경우 평균이 39.5, 표준편차가 19.47임과 전체에 대한 평균과 표준편차를 알 수 있습니다.

3.5 신뢰도분석

신뢰도는 한 대상을 유사한 측정도구로 여러 번 측정하거나 한 가지 측정도구로 반복 측정했을 때 일관성 있는 결과를 얻어내는 정도를 말합니다.

신뢰도의 동의어로는 의존성, 안정성, 일관성, 예측가능성, 정확성 등이 있습니다. 척도의 신뢰성을 평가하는 방법에는

내적일관성(internal consistency), 반복측정 신뢰성(test - retest reliability), 대안항목 신뢰성(alternative - form reliability) 등이 있습니다.

이 중에서 가장 많이 사용하는 것이 내적일관성으로 한 개념을 많은 항목으로 측정했을 때 그 항목들에 대한 일관성이나 동질성 정도를 측정하는

것으로 항목들간의 상관관계(반분법)를 통해 평가되는데 상관관계가 높을수록 내적일관성이 높고, 상관관계가 낮을수록 내적일관성이 낮다고 평가합니다.

내적일관성을 평가하기 위해서는 크론바하 알파(Chronbach's α) 계수를 이용합니다. 이 방법을 이용하여 해당 척도를 구성하고 있는

각 항목들의 신뢰성까지 평가할 수 있습니다. 크론바하 알파계수를 구하는 공식은 다음과 같습니다.

크론바하 알파계수는 0～1 사이의 값을 가지며, 값이 높을수록 바람직하나 그에 대한 기준은 학자마다 다르므로 반드시 몇 점 이상의 기준은 없습니다.

대개 0.8～0.9 사이 값이라면 신뢰도가 상당히 높다고 할 수 있고 0.7 이상이면 바람직하다고 봅니다. 0.6 이상이면 수용할 정도 수준이고,

0.6 이하이면 내적일관성을 결여한 것으로 받아들여집니다. 0.6 이하의 점수인 항목이 있으면 그 항목은 전체 항목과 일관성.

즉, 상관관계가 낮은 항목이므로 제거해야 합니다.

신뢰도 계수를 증가시키는 방법으로는 6가지가 있습니다.

① 측정항목을 많이 늘려야 합니다. 측정항목이 많아질수록 신뢰도는 증가합니다.

② 측정도구를 구체화해야 합니다. 설문지의 문항별 설명을 명확히 하여 응답자별로 해석상의 차이가 발생하지 않도록 합니다.

③ 기존에 신뢰성이 높다고 판명되어 있는 측정도구를 사용하면, 오차를 줄일 수 있습니다.

④ 응답자의 태도가 일관되도록 해야 합니다. 만일 일관되지 않게 응답하거나 성실하게 응답하지 않은 설문지는 제외시켜야 합니다.

⑤ 코딩과 펀칭 같은 자료처리 과정에서 검증을 강화하여 자료처리상의 오류를 줄여야 합니다. 만일 역점수로 측정한 경우에는 리코딩을 하여

척도의 방향을 동일하게 해주고 나서 신뢰도 검정을 해야하는 것을 잊으면 안됩니다.

⑥ 크론바하 알파계수가 낮게 나온 항목은 제거하고 나서 다시 신뢰도를 측정하면 신뢰도가 높게 나타납니다.

1) 시작방법

[예제 05-1] 파일을 열어 신뢰도 분석을 같이 해 봅시다.

신뢰도 분석을 하기 위해서는 다음과 같은 절차를 따릅니다.

　

분석(A)→척도화분석(A)→신뢰도분석(R)

이와 같은 절차를 따르면 [그림 3.14]와 같은 대화상자가 나타납니다. 대화상자에는 문항(I)칸, 모형(M), 문항설명표시(L), 통계량으로 구성되어 있습니다.

① 문항(I)/모형(M)/문항설명표시(L)

종 류	내 용
문항(I)	신뢰도를 구할 변수를 이동하는 칸입니다. 이 칸으로 신뢰도를 구하고 싶은 변수를 옮겨놓습니다.
모형(M)	모형에서는 신뢰도를 평가하는 방법에 대한 것을 설정하는 것입니다.
문항설명표시(L)	변수에 설명이 되어있는 경우 그 설명을 출력해 줍니다.

② 통계량(S)

여기서는 기술통계의 내용을 설정할 수 있는데 보통은 신뢰도를 저하시키는 변수들을 찾아낼

수 있는 정보를 얻을 수 있습니다. 통계량에는 다음에 대한 기술통계량과 요약값, 문항-내, 분산분석표로 구성되어 있습니다. 이에 대해서 다음 표로 자세히 설명하겠습니다.

종 류		내 용
다음에 대한 기술통계량	문항(I)	맨 왼쪽의 변수 하나를 제외한 모든 변수 값의 합의 평균을 나타냅니다.
	척도(S)	맨 왼쪽의 변수 하나를 제외한 모든 변수 값을 합하였을 때의 분산을 알려줍니다.
	문항제거시 척도(A)	맨 왼쪽의 변수 하나를 제외하였을 때 크론바하 알파계수를 알려줍니다.
요약값		각 변수의 평균, 분산, 공분산, 상관관계를 구할 수 있습니다.
문항-내		각 변수간의 상관관계와 공분산을 구할 수 있습니다.
분산분석표		F검정이나 카이제곱 검정 Table를 구할 수 있습니다.

2) 실행방법

문항과 통계량 등을 설정한 후 확인을 누르면 [그림 3.16]과 같은 출력결과가 나타납니다.

[그림 3.16]에서 보면 현 상태에서는 Chronbach's α 값이 Alpha = .8251으로 맨 아래에 나타나있고, 각 항목별로 제거하면

기대되는 Chronbach's α 값이각 항목별 우측 맨 끝에 나타나 있습니다. 값이 가장 큰 변수는 A6_1로 그에 대한 Chronbach's α 값은

.8334로 그 변수를 제거하면 Chronbach's α 값이 .8334로 증가하므로 변수A6_1를 제거하는 것이 좋습니다.

그러나 전반적인 Chronbach's α 값이 Alpha = .8251이므로 굳이 제거할 변수는 없습니다.

그림 3.1) 신뢰성분석 결과

****** Method 1 (space saver) will be used for this analysis ******

R E L I A B I L I T Y   A N A L Y S I S   -   S C A L E   (A L P H A)

                             Mean        Std Dev       Cases

1.     A6_1              2.5667          .8584        30.0
2.     A6_2              2.5333         1.0417        30.0
3.     A6_3              2.5333          .8193        30.0
4.     A6_4              3.3000          .9879        30.0
5.     A6_5              3.6667          .8841        30.0
6.     A6_6              2.2333          .9714        30.0

                                                   N of
Statistics for       Mean   Variance    Std Dev Variables
      SCALE       16.8333    16.6264     4.0776          6

Item-total Statistics

               Scale          Scale      Corrected
               Mean         Variance       Item-            Alpha
              if Item        if Item       Total           if Item
              Deleted        Deleted    Correlation        Deleted

A6_1          14.2667        13.3747        .4006           .8334
A6_2          14.3000        10.6310        .7229           .7668
A6_3          14.3000        12.0793        .6806           .7819
A6_4          13.5333        11.7747        .5717           .8022
A6_5          13.1667        12.4885        .5371           .8083
A6_6          14.6000        11.3517        .6616           .7819

Reliability Coefficients

N of Cases =     30.0                    N of Items = 6
Alpha =    .8251

4. 복수응답 분석

복수응답이란? 하나의 질문에 응답결과가 여러 개 나와있는 경우를 말합니다. 예를 들어 ‘귀하가 좋아하는 색상을 모두 고르시오’ 와

같은 문항을 분석하는 방법입니다. 그러면 복수응답을 분석하는 방법에 대해 공부해 봅시다.

　

♠ 복수응답을 분석하기 위한 방법
① 범주형(Categories) : 선택된 변수값만 코딩하는 방법
② 양분형(Dichotomies) : Yes나 No처럼 둘 중에 하나는 선택하고 하나는 선택하 지 않는 방법
③ 우선순위 분석방법 : 각 항목에 따라 가중치를 주어 분석하는 방법

우선순위 분석방법에 대해 더 자세히 알아봅시다.

① 각 항목에서 순위를 결정합니다.

예를 들면 ‘다음 4가지 음료수 중 어떤 음료수를 좋아하는지 가장 좋아하는 것을 찾아 순서대로 순위를 매겨 주십시오.’라는

질문에 1순위에서는 탄산음료가 9명, 커피가 5명이 응답하였고, 2순위에서는 탄산음료는 3명, 홍차가 5명, 커피가 7명으로 응답을 하였고,

3순위에서는 탄산음료가 3명, 홍차가 4명, 커피가 5명으로 응답했다면, 이를 통해 대강 순위를 매길 수 있습니다. 여기서는

탄산음료가 1순위, 커피가 2순위, 홍차가 3순위로 볼 수 있습니다.

② 각 순위별로 가중치에 대한 비율을 결정하여 각 항목에 대한 값을 정합니다.

가중치에 대한 비율은 연구자의 타당성 있는 근거나 순위에 대한 중요성을 부각시킬 경우 다르게 주어질 수 있습니다.

그러면 일반적인 경우에 정하는 가중치 비율로 항목 값을 계산해 봅시다.

1순위는 300%, 2순위는 200%, 3순위는 100%의 가중치를 준다고 한다면, 탄산음료는 9명×300% + 3명×200% + 3×100% = 36점,

홍차는 5×200% + 4×100% = 14점, 커피는 5×300% + 7×200% + 5×100% = 34점으로 나타납니다.

이렇게 나온 값에 의해 순위가 결정됩니다.

4.1 범주형 자료의 분석

범주형 자료 분석을 하기 위한 방법에 대해 살펴봅시다. 아래의 설문지의 경우 2가지를 선택하게 되어 있으므로,

선택변수는 2가지이고, 하나의 선택변수마다 1～8까지의 응답범위가 있습니다.

♠ 귀하가 생각하기에 배우자의 결혼 조건으로 가장 중요한 것은 무엇이라고 생각하십니까? 가장 중요한 것을 2가지만 응답해 주세요.     (       ,      )
① 직업 ② 성격         ③ 학벌         ④ 건강
⑤ 외모 ⑥ 가문         ⑦ 경제수준      ⑧ 기타(          )

1) 코딩방법

선택변수가 두 개이므로 변수 칸을 두 줄로 설정해야 합니다. 위의 설문에 대해 코딩한 값은 [예제 06-1] 파일에 있습니다.

그 파일을 불러오면 [그림 4.1]과 같은 창이 나타납니다.

[그림 4.1]에서와 같이 하나의 질문에 대한 변수를 두 개로 구분해서 코딩한 것을 볼 수 있습니다.

2) 변수군 정의

두 개로 구분한 변수를 하나로 정의하는 방법에 대해 살펴봅시다.

분석(A)→다중응답분석(L)→변수군 정의(D)

다음과 같은 절차를 따라하면 [그림 4.2]와 같은 창이 나타납니다.

변수군 정의에 칸에 있는 변수를 변수군에 포함할 변수(V)에 옮겨 놓습니다. 변수군의 고정형식에서는 범주형자료를 분석하고 있으므로

[◉범주형]에 클릭을 하고 범위에 1과 8을 입력합니다. [이름(N)]에는 자신이 원하는 변수명을 입력하고

[설명(L)]에는 그 변수에 대한 설명을 입력한 후 추가를 누르면 됩니다. 그런 다음 [닫기]를 누릅니다.

3) 실행방법

변수군에 대한 정의를 해 주었으므로 그 변수군을 가지고 복수응답에 대한 분석을 실행해야 합니다. 실행을 하기 위해 다음과 같은 절차를 따라 합니다.

분석(A)→다중응답분석(L)→빈도분석(F)

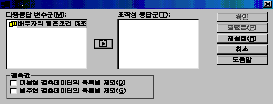
이 절차를 거치면 [그림 4.3]과 같은 창이 나타납니다.

다중응답 변수군(M)에 있는 변수군을 표작성 응답군(T)로 옮깁니다. 결측값이 있는 경우에는 범주형 결측데이터의 목록별 제외여부를 선택하고

확인을 누르면 다음과 같은 결과가 나타납니다.

다중응답분석

Group $조건 배우자의 결혼 조건

                                                           Pct of Pct of
Category label                          Code      Count Responses Cases
직업                                       1          8     13.3     26.7
성격                                       2         10     16.7     33.3
학벌                                       3          7     11.7     23.3
건강                                       4          7     11.7     23.3
외모                                       5          9     15.0     30.0
가문                                       6          8     13.3     26.7
경제수준                                   7          5      8.3     16.7
기타                                       8          6     10.0     20.0
                                                -------    -----    -----
                               Total responses       60    100.0    200.0

0 missing cases; 30 valid cases

[Group $조건 배우자의 결혼 조건] - 새로 지정한 변수군 명

[0 missing cases; 30 valid cases] - 둘 다 응답한 사람이 30명이고, 둘 다 응답하지 않은 사람이 0이라는 것을 말합니다.

[Count] - 총 응답한 수를 말하는 것으로, 여기서는 30명이 모두 다 2개씩 응답한 것을 볼 수 있고, 각 보기에 따라 응답한 빈도가 나타나 있습니다.

[Pct of Responses] - 응답 개수에 대한 백분율(%)을 말하는 것으로 총 합계 60을 100%로 볼 때 그 빈도(Count)에 대한 비율을 말합니다.

[Pct of Cases] - 응답 사례에 대한 백분율(%)을 말하는 것으로 총 응답자 수 30명을 가지고 볼 때 그 빈도(Count)에 대한 비율을 말합니다.

4.2 선택형 자료의 분석

선택형 자료 분석을 하기 위한 방법에 대해 살펴봅시다.

1. 귀하의 성별은?
① 남자 ② 여자
2. 귀하의 연령은?
① 30세 이하 ②31～40세 ③ 41～50세
④ 51～60세 ⑤ 61～70세 ⑥ 71세 이상
3. 귀하는 퇴직교육 프로그램을 실시한다고 할 때 어떤 방식의 교육방법을 선호하십니까? 해당하는 것을 모두 고르세요.
① 각 분야별 전문가로 구성된 강의 중심
② 학습자 상호간의 정보 교환을 통한 토론 중심
③ 퇴직 지원의 창업 성공사례 소개 및 토론
④ 영화, 슬라이드 등을 활용한 시청각 교육
⑤ 인터넷을 통한 동영상 강의

설문지 3번 문항과 같은 경우 선택형 자료 분석을 해야 합니다. 1～5개의 항목을 나열한 후 그 중에 자신에게 해당하는 것을 고르는

질문이나 실제로는 5문항을 물어보는 것과 동일하다고 생각하시면 됩니다.

1) 코딩방법

3번 문항을 코딩을 하기 위한 문항으로 만들어보면 다음과 같습니다.

　

1. 퇴직교육 프로그램을 실시할 때 각 분야별 전문가로 구성된 강의 중심의 교육방법을 선호하십니까?             ① 예   ② 아니오
2. 퇴직교육 프로그램을 실시할 때 학습자 상호간의 정보 교환을 통한 토론 중심의 교육방법을 선호하십니까?       ① 예   ② 아니오
3. 퇴직교육 프로그램을 실시할 때 퇴직 지원의 창업 성공사례 소개 및 토론의 교육방법을 선호하십니까?          ① 예   ② 아니오
4. 퇴직교육 프로그램을 실시할 때 영화, 슬라이드 등을 활용한 시청각 교육의 교육방법을 선호하십니까?            ① 예   ② 아니오
5. 퇴직교육 프로그램을 실시할 때 인터넷을 통한 동영상 강의 중심의 교육방법을 선호하십니까?         ① 예   ② 아니오

이렇게 바꾼 문항을 코딩하려면 [예]와 [아니오] 둘 중에서 하나를 선택합니다. [예]를 선택하고자 하면 [예]를 1로 [아니오]를

0으로 하여 코딩하면 됩니다. [아니오]를 2로 입력해도 되지만 처리가 용이하기 위해서는 0으로 하는 것이 좋습니다.

이를 토대로 입력된 코딩은 [예제 06-2] 파일에 있습니다. 그 파일을 열어보면 [그림 4.4]와 같은 창이 나타납니다.

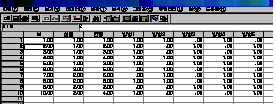
[그림 4.4]와 같이 5개로 구분해서 코딩한 것을 볼 수 있습니다. 물론 값은 0과 1로 구성되어 있습니다.

2) 변수군 정의

변수군을 정의해 주기 전에 코딩한 값에 대한 각 변수마다의 설명을 해 주어야 합니다. [변수보기]창으로 가서 [값]을 클릭하면

…
가 나오는데 그것을 클릭하면 [그림 4.5]와 같은 대화상자가 나타납니다.

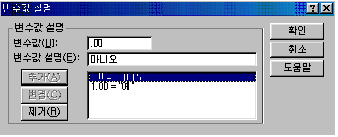
변수값 0과 1에 대한 변수값 설명을 해 준 후 확인을 누릅니다.

그러면 이제, 변수군을 설정해 봅시다. 다섯 개로 구성되어 있는 변수를 하나로 정의해야 하는데 그 절차는 범주형분석에서 한 것과 동일합니다.

　

분석(A)→다중응답분석(L)→변수군 정의(D)

다음과 같은 절차를 따라하면 [그림 4.6]와 같은 대화상자가 나타납니다.

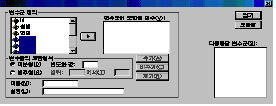
정의해 주어야할 변수군을 변수군에 포함된 변수(V)에 옮깁니다. 여기서는 방법1～방법5에 관한 변수를 옮겨주면 됩니다.

여기서의 분석은 선택형자료이므로 변수들의 코딩형식을 [◉이분형]으로 설정해 주고 그 빈도화 값에는 [예]를 1로 선택하였으므로 1을 입력해 줍니다.

변수이름(N)과 설명(L)에 각각 원하는 것을 입력한 후 [추가]를 누르고 나서 [닫기]를 누릅니다.

3) 실행방법

　

분석(A)→다중응답분석(L)→빈도분석(F)

이 절차를 거치면 [그림 4.7]과 같은 창이 나타납니다.

[그림 4.7]에서 다중응답 변수군(M)에 있는 변수를 표작성 응답군(T)으로 옮긴 후 [확인]을 누르면 다음과 같은 결과 창이 나타납니다.

　

다중응답분석

Group $방법들 퇴직교육방법
     (Value tabulated = 1)

                                                          Pct of Pct of
Dichotomy label                       Name       Count Responses Cases
                                      방법1          7     22.6     70.0
                                      방법2          5     16.1     50.0
                                      방법3          5     16.1     50.0
                                      방법4          7     22.6     70.0
                                      방법5          7     22.6     70.0
                                               -------    -----    -----
                              Total responses       31    100.0    310.0

0 missing cases; 10 valid cases

[Value tabulated = 1] - 선택된 변수값이 1임을 알려줍니다. 변수군을 정의해 줄 때 빈도화 값에 1을 입력해 준 결과입니다.

[Dichotomy label] - 각 변수명에 대한 설명을 나타내는데, 여기서는 변수명에 대한 설명을 설정해 주지 않아 아무 명이 없습니다.

변수명에 대한 설명을 설정해 주면 Dichotomy label에 그 이름이 나타납니다.

[Name] - 각 변수에 대한 이름입니다.

[0 missing cases; 10 valid cases] - 총 응답자가 10명이며, 응답을 하지 않은 사람이 0명이라는 것을 알 수 있습니다.

[Count] - 응답자 10명이 방법1～방법5까지 응답한 빈도를 나타내며, Total에서의 31은 10명의 응답자가 총 31개를 응답했다는 것을 알 수 있습니다.

[Pct of Response] - 응답자가 대답한 31개의 개수를 100%로 하여 그에 대한 항목별로의 빈도별 백분율을 나타낸 것입니다.

[Pct of Cases] - 응답 사례에 대한 백분율(%)을 말하는 것으로 응답률이 310%이고 응답자 수가 10명이므로 한 사람 당 3.1개씩 응답했다고 볼 수 있습니다.

4.3 복수응답에서의 교차분석

선택적 자료에서의 설문지를 보게 되면 성별, 연령, 퇴직교육방법 등 총 3문항으로 물어보고 있습니다. 여기서 성별에 따른 퇴직교육방법이라든지,

연령에 따른 퇴직교육방법 등을 분석해 보고자 하는 경우에 어떻게 해야 하는지 알아보고자 합니다. 연습을 위해 [예제 06-3]의 데이터를 가져옵시다.

선택적 자료 분석에서와 똑같이 변수군을 정의해 줍니다. 변수군 정의 절차는 분석(A)→다중응답분석(L)→변수군 정의(D)인거 아시죠? 자,

그러면 복수응답에서의 교차분석을 시작해 봅시다.

1) 실행방법

성별에 따른 퇴직교육방법에 관한 복수응답 교차분석을 실행하기 위해 다음과 같은 절차를 따라 합니다.

　

분석(A)→다중응답분석(L)→교차분석(C)

이 절차를 거치면 [그림 4.8]과 같은 대화상자가 나타납니다.

대화상자가 나타나면 다중응답 변수군(M)에 있는 퇴직교육방법 [$ 방법들]을 행(W)으로 옮기고 성별을 열(N)로 옮깁니다.

성별을 열(N)로 옮기게 되면 [성별(??)]이 나타나면서 [범위지정(G)] 단추도 동시에 나타납니다. [범위지정(G)]를 클릭하면, [그림 4.9]가 나타납니다.

성별에서의 값이 1과 2로 최소값이 1이고 최대값이 2이므로 1과 2를 입력한 후 계속을 누릅니다. 다시 [그림 4.8]로 돌아오면, 옵션(O)을

설정해 주는데 [그림 4.10]과 같은 대화상자가 나타납니다.

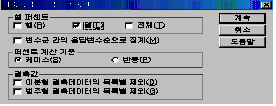
옵션(O)에는 크게 [셀 퍼센트]와 [퍼센트 계산 기준], [결측값]으로 구분되어 있는데, 우선은 행(R)과 열(L) 중에서 퍼센트(%)로 지정하고 싶은 것에 클릭을 합니다.

여기서는 열(L)만 설정해 봅시다. 시간이 되면 여러 방법으로 실행을 해 보세요.

퍼센트 계산 기준에서는 기준을 케이스(S)로 할지 반응(P)으로 할지 결정해서 설정해야 합니다. 기준을 설정함에 따라

Column Total 이 달라지므로 잘 선택하여 [계속]을 누른 후 [확인]을 누르면 다음과 같은 결과 창이 나타납니다.

* * * C R O S S T A B U L A T I O N * * *

$방법들 (tabulating 1) 퇴직교육방법 by 성별

성별

Count o남 여

Col pct o Row

o Total

o 1 o 2 o

$방법들 -----------------------------------

방법1 o 5 o 2 o 7

o 100.0 o 40.0 o 70.0

-----------------------------------

방법2 o 2 o 3 o 5

o 40.0 o 60.0 o 50.0

-----------------------------------

방법3 o 4 o 1 o 5

o 80.0 o 20.0 o 50.0

-----------------------------------

방법4 o 3 o 4 o 7

o 60.0 o 80.0 o 70.0

-----------------------------------

방법5 o 3 o 4 o 7

o 60.0 o 80.0 o 70.0

-----------------------------------

Column 5 5 10

Total 50.0 50.0 100.0

Percents and totals based on respondents

10 valid cases; 0 missing cases

[10 valid cases; 0 missing cases] - 총 응답자 수가 10명이고 무응답 수가 0명임을 알 수 있습니다.

[Column Total] - 여기서는 이 전에 [열(L)]를 선택하였으므로, 세로로 구성된 값만 보면 됩니다. 그 값이 바로 Column Total이고,

남자 5명, 여자 5명, 총 10명이 응답한 것을 알 수 있습니다. 방법에 따라 부분적으로 살펴보면, 방법1의 경우 남자는 5명이

모두 [예]라고 응답하였으며, 여자는 2명만이 [예]라고 응답한 것을 알 수 있습니다.

4.4 복수응답의 명령어 저장

복수응답의 경우 SPSS 프로그램을 종료하면 SPSS 데이터 편집기에 자료들이 남아 있는 것이 아니기 때문에 복수응답에

대한 자료가 상실되므로 따로 저장을 해 주어야 합니다. 복수응답에 대한 자료가 상실되면 다음에 또 복수응답에 대한 것들을

다시 설정해 주어야 하기 때문에 많은 번거로움이 있으므로 저장을 해 두었다가 다시 불러서 사용하는 것이 좋습니다.

그러면, 복수응답에 대한 명령어를 저장하는 방법에 대해서 알아봅시다. 명령어를 저장하기 위해서 복수응답 교차분석 대화상자로

되돌아 가보면 [확인] 아래에 [명령문(P)]가 있습니다. 그것을 클릭하면 [그림 4.11]처럼 SPSS 명령문 편집기 창이 나타납니다.

편집기 창이 나타나면 바로 파일(F)에서 저장(S)을 합니다.

이것을 다시 사용하고 싶을 때 불러오는 방법은 파일(F)→열기(O)→명령문(S)의 절차를 따르면 [그림 4.12]와 같은 대화상자가 나타납니다.

대화상자에서 불러오고 싶은 명령문을 선택한 후 [열기]를 누르면, 다시 [그림 4.11]과 같은 SPSS 명령문 편집기 창이 나타납니다.

SPSS 명령문 편집기를 실행하여 이전에 분석한 것들을 보고자 할 때는 실행(R)의 메뉴 중 원하는 것을 선택하여 실행하시면 됩니다.

모두(A)	Syntax - SPSS 명령문 편집기 창의 모든 명령어를 수행합니다.
선택영역(S)	마우스로 블록을 설정한 영역만 명령어를 수행합니다.
현재(C)	현재 커서가 있는 곳에서만 명령어를 수행합니다.
끝까지(T)	커서부터 명령어 끝까지 명령어를 수행합니다.