|
카이검증
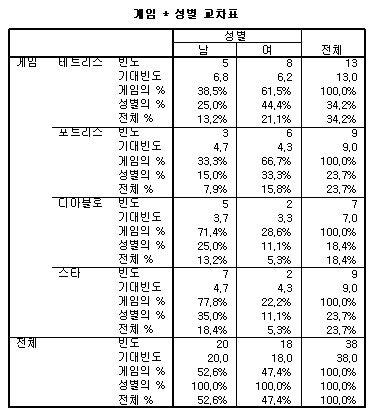
게임*성별
교차표에서는 관측빈도와 기대빈도, 각 빈도별 퍼센트가 나타나 있습니다.
카이제곱
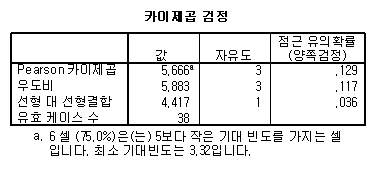
검정표에서는 카이제곱(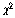 )값과
유의확률(p-value)이 나타나있습니다. 여기서는 Pearson의 카이제곱 값이 5.666이고 유의확률이 0.129이므로 )값과
유의확률(p-value)이 나타나있습니다. 여기서는 Pearson의 카이제곱 값이 5.666이고 유의확률이 0.129이므로 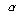 =0.05보다 크므로 영가설을 기각할 수 없습니다.
결론적으로 “남녀간의 선호하는 게임의 종류에 차이가 없다”고 할 수 있습니다. =0.05보다 크므로 영가설을 기각할 수 없습니다.
결론적으로 “남녀간의 선호하는 게임의 종류에 차이가 없다”고 할 수 있습니다.

대칭적
측도에서의 분할계수는 0.360으로 두 변수와의 관계가 약간 작은 편이라고 할 수 있습니다.
5.2
적합도 검증(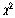 ) )
1)
개념
적합도
검증(chi-square goodness of fit test)은 어떤 조건에서 기대되는 빈도에 관측빈도가 얼마나 적합한가를 조사하는데 사용하는
방법입니다. 따라서 우리의 관심사는 영가설에서 제시한 각 칸의 비율이 실제 자료에 적합한지를 알아보는 것입니다. 위의 관심사를 알아보기 위해
다음과 같은 가설을 통해 분석을 하여 봅시다.
2)
가설검증
가구회사에서
조사자가 가구 색에 대한 소비자들의 선호도를 알아보기 위해 최근에 팔린 가구 색을 조사해 본다고 하자.
<연구가설>
: 소비자들의 색깔에 대한 선호도에는 차이가 있다.
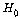 (영가설) : 소비자들의 색깔에 대한 선호도에는 차이가
없다. (영가설) : 소비자들의 색깔에 대한 선호도에는 차이가
없다.
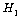 (대립가설) : 소비자들의 색깔에 대한 선호도에는 차이가
있다. (대립가설) : 소비자들의 색깔에 대한 선호도에는 차이가
있다.
이에
대한 카이스퀘어(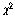 ) 통계량 계산은 독립성 검증과
비슷하므로 생략을 하고 선호도의 차이에 대한 실행방법으로 넘어가겠습니다. ) 통계량 계산은 독립성 검증과
비슷하므로 생략을 하고 선호도의 차이에 대한 실행방법으로 넘어가겠습니다.
3)
실행방법
카이검증을
하기 위한 절차는 다음과 같습니다. [예제 07-2] 파일을 열어 다음을 따라해 봅시다.
이와
같은 절차를 하게 되면 [그림 5.6]과 같은 대화상자가 나타납니다.
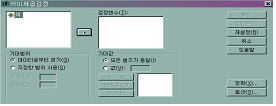
그림
5.6 적합도 검증
우선,
변수 목록 창에 있는 변수를 검정변수(T)로 옮깁니다. 그런 다음에 기대범위와 기댓값, 정확(X), 옵션(O) 등을 설정해 줍니다. 그에 대한
설명을 자세히 하면 다음과 같습니다.
①
기대범위
|
데이터로부터
읽기(G) |
각
개별값을 범주로 정의해 줍니다. |
|
지정한
범위 사용(S) |
특정한
범위내의 검증 변수값을 갖는 케이스들에 대해서만 분석하도록 검증 변수값의 하한과 상한을 지정해 줄 수 있습니다. 검증변수의 범위 밖에
있는 값은 케이스 분석에서 제외됩니다. |
②
기대값
모든
범주들이 동일한 기대값을 가지는 것으로 가정할 때 사용합니다.
③
정확(X)
앞의
독립성 검증과 동일합니다.
④
옵션(O)
[그림
5.7]과 같은 대화상자가 나타나면, 자신이 원하는 통계량과 결측값을 설정하면 됩니다.
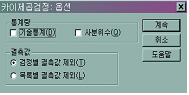
그림
5.7 적합도 검증 - 옵션
|
결측값 |
검정별
결측값 제외(T) |
해당
검증과 관련이 있는 변수에서 결측값이 있는 경우 그 케이스를 분석에서 제외시킵니다. |
|
목록별
결측값 제외(L) |
결측값이
있는 모든 케이스를 분석에서 제외시킵니다. |
이와
같은 설정을 한 후 [계속]을 누른 후 [확인]을 누르면 다음과 같은 결과 창이 나타납니다.

이
표에서는 관측수와 기대빈도, 잔차에 대한 값들이 제시되어 있습니다.

이
검정 통계량 표에서 보면 카이제곱 값이 9.750이고, p-value가 0.045이므로 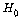 (소비자들의 색깔에 대한 선호도에는 차이가 없다)은 (소비자들의 색깔에 대한 선호도에는 차이가 없다)은 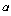 =0.05에서 기각됩니다. 따라서 소비자들의 색깔에 대한
선호도에는 차이가 있을 것이라고 분석할 수 있습니다. =0.05에서 기각됩니다. 따라서 소비자들의 색깔에 대한
선호도에는 차이가 있을 것이라고 분석할 수 있습니다.
|