9. 상관관계분석

1) 상관관계의 의미

상관계수 : 등간척도 이상의 두 변수 중에서 한 변수의 변화가 다른 변수의 변화에 따라 어떤 변화가 일어나는지를 보여주는 지표입니다.

상관관계 : 한 변수의 변화에 따른 다른 변수의 변화 정도와 방향을 예측하는 분석기법입니다.

2) 상관계수의 특징

① 변수간의 관계의 정도와 방향을 하나의 수치로 요약해 주는 지수입니다.

② 상관계수는 -1.00에서 +1.00 사이의 값을 가집니다.

③ 변수와의 방향은 (-)와 (+)로 표현합니다. 양의 상관관계일 경우에는 (+)값이 나타나고, 음의 상관관계의 경우에는 (-)값이 나타납니다. 양의 상관관계는 한 변수가 증가함에 따라 다른 변수도 증가하는 경우를 말하며, 음의 상관관계는 한 변수가 증가함에 따라 다른 변수는 감소하는 경우를 말합니다.

④ 상관계수의 절대값이 높을수록 두 변수간의 관계가 높다고 할 수 있습니다. 그러나 계수의 절대값이 작다고 해서 그 가치가 중요하지 않다고는 말할 수 없으므로 함부로 자료를 버리는 것보다 다양한 분석기법을 사용해 보는 것이 좋습니다.

상관계수	상관관계
±0.9 이상	상관관계가 아주 높다
±0.7～0.9	상관관계가 높다
±0.4～0.7	상관관계가 있다
±0.2～0.4	상관관계가 있으나 낮다
±0.2 미만	상관관계가 거의 없다

②

①

③

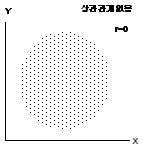
④

⑤

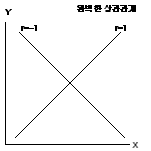
① 두 변수가 직선의 관계이면 상관계수는 ±1이 됩니다. 이런 경우를 완벽한 상관관계라고 하는데 이런 경우는 거의 드물죠? 완벽한 상관관계의 경우 두 변수간의 관계가 상당한 연관성이 있다고 보면 됩니다. 뱡향에 따라 한 쪽이 증가할 때 다른 한 쪽도 증가하면 양의 상관관계, 한쪽이 증가할 때 다른 한 쪽이 감소하면 음의 상관관계라고 할 수 있습니다.

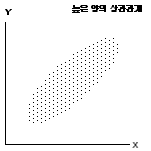
② 두 변수간의 연관성이 있다면 이러한 그래프가 나올 가능성이 큽니다. 이런 그래프가 나타난다면 두 변수간의 상관관계가 높다고 평가할 수 있습니다. 이런 형태로 기울기가 반대라면 그것은 음의 상관관계가 높다고 생각하시면 됩니다.

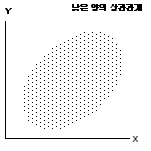
③ 두 변수의 상관관계가 낮은 경우에는 그 분포가 원에 가까워지게 됩니다. 여기서는 상관관계가 낮다고 볼 수 있는데 그래도 원형이 아니라 어느 정도 분포가 나타나므로 이러한 경향이 있다는 것 자체가 사회과학에서는 중요한 의미를 가질 수도 있습니다.

④ 이런 경우 두 변수간에 상관관계가 없다고 보면 됩니다.

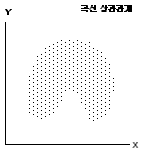
⑤ 이 그래프와 같이 ∪자와 ∩자, ―자, ｜자 등도 상관관계가 없다고 나타납니다. 그러나 ∪자와 ∩자의 형태가 나타나는 경우에는 상관비(η, 이타) 등을 구해야 합니다. 우선 두 변수가 선형관계를 얼마나 갖는지, 선형관계를 갖는다면 어느 방향인지, 그리고 그 관계는 얼마나 큰지를 분석합니다.

3) 상관관계의 성격

① 상관관계는 인과관계가 아닐 수도 있다는 것에 주의해야 합니다.

② 특별한 경우를 제외하면 상관관계는 대체로 음의 방향인지, 양의 방향인지 관계의 방향이 포함되어 있습니다.

③ 상관관계의 계수는 두 변수 관계의 상관성에 대한 예측의 정확도를 나타내는 것입니다.

④ 측정치가 아닌 하나의 지수이기 때문에 변수간의 관계의 비율이나 백분율은 다릅니다.

① ⑤ 상관관계의 계수끼리는 가감승제(±,×,÷)가 불가능합니다.

② ⑥ 상관관계의 결정계수는 상관관계의 계수를 제곱하여 나오는 값입니다.

4) 상관관계의 종류와 자료

상관계수에는 Pearson 상관계수, Spearman 상관계수, Kendall의 tau, Point biserial, Phi-coefficient가 있습니다. 다음은 척도에 따른 상관계수의 종류에 대한 것입니다.

	비연속적 명목척도	연속적 명목척도	서열척도	등간?비율척도
비연속적 명목척도	Phi계수, 유관계수, Lambda
연속적 명목척도	Yule's Q	사분 상관계수
서열척도	등위 양분 상관관계		Spearman의 서열상관계수, Kendall의 tau
등간?비율척도	Cramer's V, 양류 상관관계, 상관비(η)	양분 상관계수		Pearson 상관계수, 상관비(η)

5) 가정

변수들의 쌍은 이변량 정규분포를 따른다고 가정합니다.

6) Pearson의 상관관계(적률 상관관계)

① 두 변수가 등간척도 이상이어야 합니다.

② 두 변수가 직선의 관계가 있어야 합니다.

③ 각 행과 열의 분산이 비슷해야 합니다.

④ 적어도 하나의 변수가 정상분포를 이루어야 합니다.

⑤ 사례수가 적을수록 신뢰도가 떨어집니다.

⑥ 상관계수는 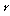로 표현합니다.

7) Spearman의 서열상관관계 및 기타 서열상관관계

① 독립변수와 종속변수가 서열척도로 구성된 경우에 사용합니다.

② 상관계수의 값은 -1.00～+1.00 사이에 있습니다.

③ 주어진 자료에서 등간성이 의문시되거나, 변수들의 점수가 극단적인 분포를 나타내는 경우에는 적률상관관계 대신 Spearman의 서열상관관계를 사용합니다.

④ 상관계수는 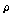로 표현합니다

⑤ Spearman의 R계수는 사례수가 많거나 두 변수간의 순위의 차이가 커서 계산이 길 때 사용합니다.

⑥ Kendall's tau(캔달의 타우)도 독립변수와 종속변수가 서열척도로 구성된 경우에 사용합니다.

⑦ 그밖에 기타 서열상관관계로는 감마, 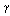또는 G, Somer's d 등이 있습니다.

8) 회귀분석과 상관관계의 차이

① 회귀분석의 경우 변수간에 인과관계가 성립되어야 합니다.

② 회귀분석은 등간성, 정규성, 선형성 등의 조건이 필요하며, 이를 검증해야 합니다.

③ 상관관계는 등간척도 이상이 아닌 서열척도만으로도 분석할 수 있습니다.

④ 상관관계는 두 변수의 관계를 예측할 수 있는 정도일 뿐 정확한 예측치를 제시하지 못합니다.

9) 검정통계량

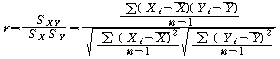
9.1 Pearson 상관관계분석

예

근무환경에 따라 직무만족도가 달라질 것이라 예상하여 그에 대한 상관관계를 알아보려고 한다.

1) 가설설정

<연구문제> 근무환경과 직무만족도 간에는 상관관계가 있다.

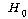(영가설) : 근무환경과 직무만족도 간에는 상관관계가 없다.

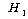(대립가설) : 근무환경과 직무만족도 간에는 상관관계가 있다.

2) 유의수준설정

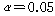
3) 실행방법

상관관계 분석을 하기 위해 [예제 11-1]를 불러 다음과 같은 절차를 따라합니다.

분석(A)→상관분석(C)→이변량 상관계수(B)

이 절차를 따르면 [그림 9.1]와 같은 대화상자가 나타납니다.

①, ② 왼쪽 변수목록 칸에 있는 변수 중 분석하고자 하는 변수를 변수(V)로 옮깁니다.

③, ④ 상관계수를 선택할 때에는 척도에 따라 등간척도 이상일 때에는 [Pearson(N)]을 서열척도일 경우에는 [Kendall의 타우-b(K)]와 [Spearman(S)]을 선택합니다. 여기서는 등간척도 이상이므로 Pearson을 선택합니다.

⑤ [유의한 상관계수 별표시(E)]라는 것은 유의미한 결과가 나왔을 때에는 결과창에 (*)표시를 해 준다는 것을 의미합니다. (*)표시가 있으면 유의미한 결과를 한 눈에 알아볼 수 있으므로 가능한 표시가 나타나도록 하는 것이 좋습니다. 유의도가 0.05 수준에서 유의한 상관관계가 나타나면 (*)표시가 나타나고, 0.01 수준에서 유의한 상관관계가 나타나면 (**)표시가 나타납니다.

⑥ 유의성 검정에서는 양측검증을 할 것이므로 [양쪽(T)]에 클릭합니다.

양쪽(T)	양측검증으로 상관관계의 방향을 설정하지 않은 경우의 검증입니다.
한쪽(L)	단측검증으로 상관관계의 방향을 설정해 준 경우의 검증입니다.

⑦ 옵션(O)

옵션에서 알맞은 통계량과 결측값 제외방식을 설정해 준 후 [계속]을 누른 다음 [확인]을 누르면 다음과 같은 결과 창이 나타납니다.

-->기술통계량

	평균	표준편차	N
근무환경	2.5974	.6174	303
직무만족	3.1814	.3966	303

기술통계량 표에서는 근무환경과 직무만족에 대한 평균과 표준편차, 사례수가 나타나 있습니다.
　

-->상관계수

		근무환경	직무만족
근무환경	Pearson 상관계수	1.000	.623(**)
	유의확률 (양쪽)	.	.000
	N	303	303
직무만족	Pearson 상관계수	.623(**)	1.000
	유의확률 (양쪽)	.000	.
	N	303	303
** 상관계수는 0.01 수준(양쪽)에서 유의합니다.

상관계수 표에서는 상관계수와 유의확률이 나타나 있습니다. 근무환경과 직무만족간의 상관관계는 .623으로 유의수준 0.001에서 높은 양의 상관관계가 나타난다고 볼 수 있습니다. 따라서 근무환경이 좋을수록 직무만족도가 높다진다고 결론 지을 수 있습니다.

9. Spearman의 서열상관관계분석

서열상관관계는 비모수 통계기법이지만 비교적 자주 사용하는 방법입니다.

예

사원들에게 퇴직교육 프로그램을 실시하려고 한다. 2명의 사람에게 교육받고 싶은 프로그램을 순서대로 번호를 매기도록 했다.

1) 가설설정

<연구문제> 두 사람의 프로그램 선호도는 관계가 있다.

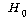(영가설) : 두 사람의 프로그램 선호도는 관계가 없다

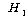(대립가설) : 두 사람의 프로그램 선호도는 관계가 있다.

2) 유의수준설정

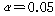
3) 실행방법

상관관계 분석을 하기 위해 [예제 11-2]를 불러 다음과 같은 절차를 따라합니다.

분석(A)→상관분석(C)→이변량 상관계수(B)

이 절차를 따르면 [그림 9.3]과 같은 대화상자가 나타납니다.

원하는 변수를 변수목록 칸에서 [변수(V)]로 옮겨준 후 [상관계수]에서 [Spearman]으로 설정해 준 다음 나머지는 Pearson과 동일하게 설정해 줍니다. 설정을 다 해 준 주 [확인]을 누르면 다음과 같은 결과 창이 나타납니다.

-->상관계수

			A	B
Spearman의 rho	A	상관계수	1.000	.791(**)
		유의확률 (양쪽)	.	.004
		N	11	11
	B	상관계수	.791(**)	1.000
		유의확률 (양쪽)	.004	.
		N	11	11
** 상관계수는 .01 수준에서 유의합니다 (양쪽).

스피어만의 서열상관계수(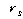)는 .791(**)이고, 유의확률은 .004로 유의수준 0.01에서 영가설이 기각됩니다. 따라서 두 사람과 프로그램 선호도와는 관계가 있다고 결론 지을 수 있습니다.

Pearson의 상관관계분석을 위해서는 변수들의 쌍은 이변량 정규분포를 따른다는 가정이 필요한 것과는 달리, Spearman 서열상관관계 분석을 하는 경우에는 주어진 자료는 서열척도로 측정된 자료이므로 이 가정을 충족시키지 못합니다. 따라서 보다 보수적인 방식으로 검증을 하는 것이 바람직합니다.

보수적인 방식으로는 [부록]의 <표 5>에 제시되어 있는 Spearman의 서열상관관계 수표를 이용합니다. 여기서 유의수준은 0.05이고 n값은 11이므로 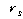의 임계치를 찾으면, 양측검정이므로 유의수준을 0.025로 하고 n을 11로 하여 그 값을 찾으면, 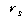의 임계치는 0.623이 됩니다. 결과치에서 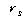값은 0.791이므로 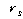임계치보다 크므로 영가설을 기각한다고 결론지으면 됩니다.

7.3 편상관관계분석

지금까지 설명한 상관관계분석은 두 변수들간의 상관관계를 살펴보았는데, 이 두 변수의 상관관계가 높다고 해서 수순히 두 변수가 인과관계에 있다고 볼 수는 없습니다. 이를 정확히 하기 위해서는 제 3의 변수를 통제해 준 상태에서 분석해야 하는데 이를 편상관관계분석이라고 합니다. 즉, 편상관관계분석은 제 3의 변수를 통제해 준 상태에서 관심을 갖는 두 변수의 관계를 분석하는 분석기법입니다. 예를 들면, 매미의 수와 아이스크림의 판매수와의 상관계수가 높다고 해서 매미의 수가 증가할수록 아이스크림의 수가 증가한다고 결론지을 수는 없습니다. 여기서는 온도(또는 계절)라는 제 3의 변수를 통제시킨다면, 아마도 두 변수의 상관계수는 달라질 것입니다.

예

본 예에서는 인관관계의 영향력을 통제한 상태에서 근무환경과 직무만족도간의 관계를 분석하고자 한다.

1) 가설설정

<연구문제> 인관관계가 일정한 경우(통제된 경우) 근무환경과 직무만족도 간에는 상관관계가 있다.

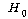(영가설) : 인관관계가 통제된 경우 근무환경과 직무만족도 간에는 상관관계가 없다.

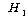(대립가설) : 인간관계가 통제된 경우 근무환경과 직무만족도 간에는 상관관계가 있다.

2) 유의수준설정

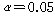
3) 실행방법

상관관계 분석을 하기 위해 [예제 11-3]를 불러 다음과 같은 절차를 따라합니다.

분석(A)→상관분석(C)→편상관계수(R)

이 절차를 따르면 [그림 9.4]와 같은 대화상자가 나타납니다.

①, ② 변수목록 칸에 있는 변수 중 분석하고자 하는 변수를 [변수(V)]로 옮깁니다.

③ 통제할 변수는 [통계변수(C)]로 옮깁니다.

④ 각 계수에 대해 확률과 자유도가 나타납니다. 유의수준 0.05에서 유의미한 결과가 나타난 계수에는 (*)표시 붙고, 유의수준 0.01에서 유의미한 결과가 나타난 계수에는 (**)표시가 붙습니다.

⑤ 단측검증을 할 경우에는 [한쪽]에 클릭하고, 양측검증을 할 경우에는 [양쪽]에 클릭을 합니다.

⑥ 옵션

옵션에서는 통계량와 결측값을 설정할 수 있습니다.

평균과 표준편차(M)	각 변수에 대해 평균, 표준편차, 결측케이스 등이 제시됩니다.
0차 상관(Z)	통제변수가 없는 경우의 상관계수를 나타내 줍니다.

위의 같은 설정을 다 해 준 후 [계속]을 누른 후 [확인]을 누르면 다음과 같은 결과 창이 나타납니다.

기술통계

Variable Mean Standard Dev Cases

근무환경 2.5974 .6174 303

직무만족 3.1814 .3966 303

인간관계 3.3746 .5102 303

기술통계 표에서는 근무환경, 직무만족, 인간관계에 대한 평균과 표준편차, 케이스의 수가 제시되어 있습니다.

단순상관계수(통제변수 없음)

Zero Order Partials

근무환경 직무만족 인간관계

근무환경 1.0000 .6230 .1414

( 0) ( 301) ( 301)

P= . P= .000 P= .014

직무만족 .6230 1.0000 .6109

( 301) ( 0) ( 301)

P= .000 P= . P= .000

인간관계 .1414 .6109 1.0000

( 301) ( 301) ( 0)

P= .014 P= .000 P= .

(Coefficient / (D.F.) / 2-tailed Significance)

" . " is printed if a coefficient cannot be computed

이 표에서는 인관관계를 통제변수로 설정해 주지 않은 경우의 상관계수가 제시되어 있습니다. 인간관계와 근무환경은 유의확률을 보면 모두 직무만족도와 높은 상관관계가 있음을 볼 수 있습니다.

[Zero Order Partials] : 통제변수가 없다는 것을 의미합니다.
　

편상관계수 (인간관계를 통제)
　

Controlling for.. 인간관계

근무환경 직무만족

근무환경 1.0000 .6847

( 0) ( 300)

P= . P= .000

직무만족 .6847 1.0000

( 300) ( 0)

P= .000 P= .

(Coefficient / (D.F.) / 2-tailed Significance)

" . " is printed if a coefficient cannot be computed

이 표에서는 인관관계를 통제변수로 하였을 때의 근무환경과 직무만족도의 상관관계를 나타낸 것입니다. 인관관계를 통제한 상관계수 값은 통제하기 이전의 값보다 근무환경과 직무만족도의 상관계수를 높게 측정된 것을 알 수 있습니다. 그러므로 근무환경과 직무만족도의 관계는 높은 양의 상관관계가 있다고 결론 지을 수 있습니다.

위의 결과뿐만 아니라 근무환경을 통제변수로 설정해 준 후 인간관계와 직무만족도 간의 상관관계를 분석해 보는 것도 좋을 듯 합니다. 한 번 연습해 보세요.